Čtení matematických značek a výrazů

Ing. Eduard Prandstetter

[Články]

(pdf)

-

IV.

Čtení logaritmů

Znakem pro logaritmy (Briggsovy nebo briggické) je log a čte se prostě „logaritmus“. Pro logaritmy přirozené (Napierovy) máme několik znaků: lg, ln, l, l nat, log nat, log_e. Znak lg je podlé normy, přijaté Jednotou čs. matematiků a fysiků v Praze. Dosud běžnější je však psaní ln nebo l. Znaků l nat, log nat a log_e se užívá málo, jen kde je toho třeba k větší jasnosti. Všechny ty znaky lze čísti jednotně „přirozený logaritmus“ nebo — není-li možná záměna s logaritmy dekadickými — rovněž prostě „logaritmus“. Kromě toho se čtou jednotlivé znaky podle svého způsobu psaní; tak znak l čteme „el“, znak ln čteme „el en“, znak lg „el gé“. Tato čtení jsou běžnější než čtení plné („přirozený logaritmus“); jsou stručná a úplně postačí ve všech případech, kde nemůže býti pochyb o pojmu čteného výrazu), t. j. nemůže se znak l, lg a ln zaměňovati za součin obecných čísel l, l, g, l, n s následujícím výrazem. Na př. vzorec L = (4 ln ^h/_r+ ¹/₂)10^-4 čteme „el se rovná (rovno) — čtyři el en — há dle er — plus jedna polovina — krát[e] deset na méně čtvrtou“. Znak l nat a log nat čteme někdy „logaritmus naturalis“; tak by ovšem bylo možno čísti i ostatní znaky pro přirozené logaritmy. Znaky l nat, log nat a znak log nečteme podle psaní, t. j. „el nat“, „log nat“ nebo „log“.

Výraz za kterýmkoliv znakem pro logaritmus se čte v druhém pádu, není-li to výraz složitý; tam totiž — jako v podobných případech při jiných početních výkonech — čteme celý následující výraz v prvním pádu, nebo, následuje-li po znaku log jako první činitel nebo člen číslo zvláštní, čteme toto číslo v příslušném pádu a ostatek výrazu v pádu prvním. Na př. log 2 čteme „logaritmus dvou“, log 5x² „logaritmus pěti iks na druhou“; výraz log (5x)² bychom ovšem čtli „logaritmus — pěti iks — na druhou“. Záměna s výrazem (log 5x)² není při správném čtení „logaritmus pěti iks — na druhou“ možná; kromě toho se mocnina logaritmu píše obyčejně tak, že se mocnitel přidává přímo ke znaku (t. j. vpravo nahoru za znakem) a čte se „logaritmus na…“ Na př. (log 5x)² by se běžně psal log² 5x [102]a četl by se „logaritmus na druhou — pěti iks“ nebo jiným způsobem, uvedeným při čtení mocnin. Výraz log (3x²—6x+5) se čte „logaritmus — tří (nebo tři) iks na druhou minus šest iks plus pět“, výraz log 5a² bx³ y² se čte „logaritmus — pěti (nebo pět) á druhé bé iks třetí ypsilon druhé“. Výrazy za znakem log můžeme čísti i jinými způsoby, jak bylo již dříve popsáno.

Je-li logaritmus násobitelem, dělitelem, jmenovatelem nebo mocnitelem, čte se znak pro logaritmus v příslušném pádu, t. j. „násobeno (děleno, lomeno) logaritmem…“, „podle (dle) logaritmu…“, „…na logaritmus…“. V posledním čtení přechází přízvuk s předložky na na slabiku lo. Na př. výraz a^{log (x + 3)} čteme „á na — logaritmus — iks plus tři“, výraz a^{log x + 3} čteme „á na — logaritmus — iks plus tři“, a výraz a^{log x} + 3 čteme „á na logaritmus iks — plus tři“.

Logaritmy se základem jiným než 10 (t. j. dekadické) nebo e (t. j. přirozené) píší se tak, že se vpravo dolů od znaku log připojí index značící příslušný základ logaritmů. Na př. log_a b čteme „logaritmus bé při základu á“. Tak lze ovšem psáti i logaritmy dekadické (jako log₁₀x) a. přirozené (jako log_ex). Kdežto u dekadických logaritmů se základ ani nepíše ani nečte, u přirozených logaritmů se někdy tohoto způsobu psaní užívá, a pak se log_e x čte buď „logaritmus iks při základu é“, nebo jako prve „přirozený logaritmus“.

Je-li za znakem pro logaritmus zlomek, upozorňujeme na tuto okolnost napřed čtením „logaritmus zlomku“ a potom po krátké pomlčce čteme zlomek některým způsobem podle výkladu o čtení zlomků. Tím zabráníme záměně se zlomkem, který by měl logaritmus jen v čitateli. Na př. log ^{5 x2-8}/_{3 x2-4} čteme správně „logaritmus zlomku — pět iks na druhou méně osm — lomeno — třemi (tři) iks na druhou méně čtyři“. Čtení „logaritmus — pět iks na druhou méně osm — lomeno — třemi (tři) iks na druhou méně čtyři“ by znamenalo výraz ^log(5x2-8)/_3x2-4. Kdybychom první výraz chtěli čísti beze slova „zlomku“, musili bychom po slově „logaritmus“ učiniti delší pomlčku, kterou bychom naznačili, že se znak logaritmus (log) vztahuje na celý výraz dále čtený.

Čtení funkcí goniometrických a cyklometrických

Funkce goniometrické označujeme znaky vzatými z jejich jmen: sinus označujeme znakem sin, kosinus cos, tangens tg (někdy, hlavně v cizojazyčných spisech, bývá znak tan nebo tang), kotangens cotg (cot nebo ctg), sekans sec, kosekans cosec. Kofunkci [103]značíme cof. Všechny tyto znaky vyslovujeme plně a také skloňujeme. Druhý pád jedn. č. je: ko-sinu, ko-tangenty, ko-sekanty. Sinus čteme obyčejně v první slabice dlouze: „sínus“ (obdobně jako při čtení znaku pro odčítání „mínus“). U kosinu se slabika si čte někdy krátce, snad proto, že je nepřízvučná. Při čtení těchto funkcí vynecháváme slovo úhel, poněvadž se již samo sebou rozumí. Neříkáme tedy — s malými výjimkami — „sinus úhlu alfa“ atp. Funkce tangens a sekans se v 1. pádě někdy čtou „tangenta, sekanta“.

Následuje-li goniometrická funkce po některém znaku pojícím se (při čtení) s jiným pádem než prvním, zůstává přes to většinou v pádu prvním. Na př. vztah tg_α =^sinα/_cosα by se měl správně čísti „tangens alfa se rovná sinu alfa lomenému kosinem alfa“; běžně se však čte „tangens alfa rovná se sinus alfa lomeno kosinus alfa“. Funkce sinus a kosinus se čtou v jiném pádu než prvním častěji než funkce ostatní, asi proto, že jména těchto funkcí nemění při skloňování kmenovou souhlásku (n), kdežto názvy ostatních funkcí mění při skloňování koncovou souhlásku s v t, a tomu se raději vyhýbáme čtením těchto funkcí jen v prvním pádu. V složitém výrazu čteme ovšem funkce sinus i kosinus jen v prvním pádu.

Obecné úhly označujeme obyčejně řeckými písmeny a jejich názvů neskloňujeme. Je-li obecný úhel násobný, t. j. je-li dán součinem zvláštního čísla a úhlu obecného (zvláštní číslo je vždy před písmenem značícím úhel, na př. 2α, 5α a p.), čteme zvláštní číslo buď v druhém pádu, podle vazby „funkce čeho“, nebo v pádu prvním, podle vazby „funkce kterého úhlu“. Na př. sin 2α = cos 3α čteme buď „sinus dvou alfa rovná se kosinu tří alfa“ nebo „sinus dvě alfa… tři alfa“.

Na vysvětlenou uvedeme několik příkladů. 1. tg (α+12°) = tg 76° 23' čteme (běžně) „tangens alfa plus dvanáct stupňů rovná se tangens sedmdesát šest stupňů třiadvacet minut“, řidčeji, třebaže správněji: „…rovná se tangentě sedmdesáti šesti stupňů dvaceti tří minut“. 2. 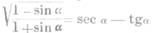 čteme (opět běžně) „odmocnina — jedna minus sinus alfa — lomeno — jedna plus sinus alfa — rovná se sekans alfa minus tangens alfa“. 3.  čteme (běžně) „jedna plus tangens alfa — na druhou — lomeno jedna plus tangens na dru[104]hou alfa — rovná se jedna plus sinus dvou (dvě) alfa“. 4. 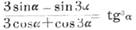 čteme „třikrát sinus (nebo „tři siny“) alfa minus sinus tři (tří) alfa — lomeno — třikrát kosinus (nebo „třemi, tři kosiny“) alfa plus kosinus tři (tří) alfa rovná se tangens na třetí alfa“. 5. 3sin²x — 4cos²x = sin x cos x čteme na př. „tři siny druhé iks méně čtyři kosiny druhé iks rovno sinu iks kosinu iks“, nebo „třikrát sinus na druhou iks minus čtyřikrát kosinus na druhou iks rovná se sinus iks kosinus iks“. 6. tg2x + tg3x = 2tgx čteme „tangens dvou (dvě) iks plus tangens tří (tři) iks rovná se dvěma (dvě) tangens iks“.

Logaritmy goniometrických funkcí čteme tak, že goniometrickou funkci čteme buď v prvním pádu (hlavně tangens a kotangens, méně sinus a kosinus), nebo v druhém pádu (sinus a kosinus, jen zřídka tangens a kotangens). Na př. log sin 25° čteme „logaritmus sinu dvaceti pěti stupňů, nebo „…sinus…“, log cotg 18° čteme „logaritmus kotangens osmnácti stupňů“, atp.

Funkce cyklometrické se označují podobně jako funkce goniometrické zkratkami svých jmen. Tak arkussinus se značí arcsin arkustangens arctg atp. Názvy tyto se neskloňují; jinak je čtení stejné jako u funkcí goniometrických.

Znaky pro funkce logaritmické, goniometrické a cyklometrické jsou sice vzaty z jejich jmen, ale nejsou zkratkami, nýbrž značkami, a proto se za nimi nedělá tečka.

Čtení indexů

Indexy se zpravidla píší vpravo dolů od obecného čísla. Index je psán ovšem menším písmem než číslo, při němž stojí.

Nejčastěji bývá index jedno zvláštní číslo a čte se pak jako prostá číslovka. Na př. a₁ čteme „á jedna“, c₀ „cé nula“, x₂ „iks dvě“ atd. Je-li index složen ze dvou zvláštních čísel, neoddělujeme tato čísla čárkou (jsou-li jednociferná) a čteme každé zvlášť. Na př. a₃₃ čteme „á tři tři“, b₁₂ „bé jedna dvě“ atp. Záměna s jediným indexem dvojciferným je takřka nemožná, neboť z textu je zřejmé, je-li index složen ze dvou jednociferných čísel, či je-li to jedno číslo dvojciferné. Je-li na př. v nějakém textu 12 (t. j. jedna, dvě), musí tam nutně býti i index 11 (jedna, jedna). Kdyby index 12 značil číslo dvanáct, musily by býti v textu také indexy aspoň od jedné až do jedenácti, t. j. indexy 1, 2, 3,…10, 11. Z takového srovnání lze snadno zjistiti hodnotu indexu. Ostatně indexy s dvojcifernými čísly se zřídka vyskytují. Skládá-li se jeden index ze dvou čísel, [105]z kterých jedno nebo obě jsou dvojciferná, oddělujeme je čárkou.

Jsou-li v jednom indexu dvě jednociferná čísla oddělená od sebe čárkou, je význam indexu jiný než prve. V takovém případě se tímto indexem naznačuje, že veličina, při které stojí, má dvě nebo několik hodnot, podle počtu čísel v indexu. Je to běžné označování neznámé veličiny, má-li tato veličina více hodnot než jednu. Na př. vzorec pro kořen kvadratické rovnice (obecné) zní 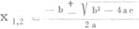 a čte se „iks jedna dvě se rovná — minus bé plus minus odmocnina — bé na druhou minus čtyři á cé — lomeno dvěma á“.

Obecných čísel — t. j. písmen — neužívá se za indexy často. Ještě nejspíše se vyskytují tam, kde se zároveň vyskytují indexy vyjádřené zvláštními čísly, a tam, kde značí obecnou, neurčitou hodnotu. Se zřetelem k tomu je při čtení záměna obecného čísla s platností indexu za činitele v součinu sotva možná. Řadu a₁+a₂+ … +a_n-1 + a_n čteme „á jedna plus á dvě plus — plus á en méně jedna — plus á en“. Vzorec pro součet aritmetické řady S_n = ⁿ/₂ (a₁+a_n) čteme „es en rovná se en půl krát [e] á jedna plus á en“. Součin 2a_mx by se četl prostě „dvě á em iks“, jestliže by poslouchající osobě bylo předem jasno, že m je index. Jinak bychom musili čísti „dvě á s indexem em krát [e] iks“, nebo stručněji „dvě á em krát [e] iks“. Toto čtení neznačí výraz 2amx, který se čte jen „dvě á em iks“. Čtení „s indexem“ lze užíti u jakýchkoliv indexů, ale užívá se ho jen tehdy, je-li nutné k bezvadnému porozumění.

Znakem pro součet jistého počtu členů nějaké řady je velké řecké písmeno sigma (Σ), s indexem pod písmenem a nad ním. Dolní index je pro první člen, horní pro člen poslední, takže je tím řada (t. j. počet členů) určena. 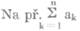 značí součet řady s členy a₁, a₂, a₃…a_k, …a_n, a čte se „součet (suma) všech á ká od ká rovno jedné až do ká rovno en“, nebo stručněji „součet všech á ká rovno jedné do en“ (nebo „… až en“). Místo slov „od… až do“ se někdy říká „pro… až“.

Znak pro součin čísel stejného druhu (lišících se jen indexem) je velké řecké písmeno pí (π). Čtení je podobné jako pro znak Σ, 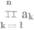 čteme „součin všech á ká od ká rovno jedné až do ká rovno en“ nebo kratčeji, jak uvedeno výše.

[106]Znak pro faktoriál čísla je vykřičník kladený hned za číslo. Čteme jej faktoriál (s 2. pádem čísla), faktoriálně nebo faktoriálných (-á, -é). Na př. 3! čteme „faktoriál tří“ nebo „tři faktoriálně (-né)“, n! čteme „faktoriál en“ atd.

Kombinační číslo tvoří dvě čísla (nebo výrazy) psaná nad sebou bez zlomkové čáry a uzavřená do závorek (okrouhlých). Hořejší číslo čtené v prvním pádu se spojuje předložkou nad s dolejším číslem, čteným v sedmém pádu. Je-li dolní výraz složitý, čte se jako v jiných podobných případech v pádu prvním. Na př. 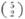 čteme „pět nad dvěma“,  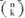„en nad ká“.  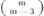„em nad em méně tři (nebo třemi)“ atd. Přízvuk se někdy posouvá s předložky nad na první vyslovenou slabiku dolního výrazu. Jeví se tu obdoba s posouváním přízvuku s předložky na při čtení mocnin.

Znak nerovnosti (≠) čteme nerovná se, není rovno. Proti čtyřem čtením znaku rovnosti máme zde jen dvě čtení. Čtení není a nerovno, která by byla záporem čtení je (jest) a rovno se neužívá. Čteme tedy na př. x ≠ 5 „iks není rovno (nerovná se) pěti“. Jinak platí totéž, co bylo uvedeno při čtení znaku rovnosti.

Znaky < a > se čtou je menší než a je větší než. Hrot šipky směřuje vždy k výrazu menšímu. Na př. a < b se čte „á je menší než bé“ a značí matematicky totéž co b > a, které se čte „bé větší než á“. Oba znaky se často vyskytují se znakem rovnosti zároveň, a máme pak tyto sdružené znaky: ≥ čteme je menší nebo rovno, ≤ čteme je větší nebo rovno, a konečně je větší, rovno nebo menší než. Slovo nebo se někdy vynechává.

Znak přibližnosti (t. j. ) se čte nejčastěji rovná se přibližně. Místo slova přibližně lze říci asi, ale toho se málo užívá. Kromě uvedeného čtení můžeme užíti i všech ostatních čtení pro znak rovnosti s dodatkem přibližně (asi).

Čtení závorek. Nejčastěji se užívá závorek okrouhlých, oblých ( ), potom hranatých (lomených) [ ]. Pak jsou ještě závorky složené { } a jiné, je-li třeba rozlišovati určité výkony nebo výrazy rozličnými závorkami. Při čtení označujeme závorky přídavným jménem určujícím je blíže jen tehdy, jsou-li ve výrazu, který čteme, aspoň dva druhy závorek. Obyčejně však označujeme přídavným jménem jen první závorku určitého druhu, protože při druhé závorce (uzavírací) není nutno adjektivum opakovati, neboť z výrazu, dosud podle čtení napsaného nebo slyšeného, bývá zřejmé, o kterou závorku právě jde.

[107]Je-li v textu jen jeden druh závorek (obyčejně okrouhlých), učiníme po posledním slovu před čtením závorky (na př. plus, minus, krát atd.) malou pomlčku, po ní řekneme „závorka“, a po další krátké pomlčce (ale tu někdy vynecháváme) čteme výraz uzavřený do závorek jako celek podle některého ze známých způsobů; následuje opět pomlčka a po ní by se mělo správně čísti „výraz se uzavře (druhou) závorkou“. Ale toto rčení by bylo příliš dlouhé, a tak se našlo stručné rčení „závorka se uzavře“. Čtení „závorka se uzavře“ lze vynechati, jestliže je z dalšího čtení ihned vidět, kam druhá závorka náleží, na př. je-li po druhé závorce znak rovnosti nebo nová závorka. Můžeme tedy čísti výraz 7x — 4(x²—2x+2) = 6 „sedm iks — minus čtyřikrát závorka — iks na druhou minus dvě iks plus dvě — rovná se šesti“; součin (4x³—3x²+2x—3) (3x²—2x+5) můžeme čísti „závorka — čtyři iks na třetí minus tři iks na druhou plus dvě iks minus tři — kráte závorka — tři iks na druhou minus dvě iks plus pět“.

Je-li v textu několik druhů závorek, nutno uváděti při čtení každé závorky i přívlastek určující její tvar. Na př. výraz y = 7x—{3x+5+2 [2x—(x+4)+l]—3}+4 budeme čísti „ypsilon se rovná sedmi (sedm) iks minus — složená závorka — tři iks plus pět plus dvakrát — lomená závorka — dvě iks minus — okrouhlá závorka — iks plus čtyři — okrouhlá závorka se uzavře — plus jedna — lomená závorka se uzavře — minus tři — složená závorka se uzavře — plus čtyři“. Čtení je dlouhé a nelze je zkracovati. V praxi ovšem zřídka kdy bývá více druhů závorek než dva, a potom v některých případech můžeme čtení zkrátiti buď vynecháním adjektiva při uzavírací závorce nebo při všech závorkách, nezáleží-li na jejich tvaru, anebo některým jiným způsobem, ke kterým nyní přijdeme.

Čtení závorek se rádi vyhýbáme. Jednak proto, že se tím celé čtení znatelně prodlužuje, jednak snad i proto, že čtení závorek — pokud ovšem není nezbytné — vypadá začátečnicky. Je právě znakem zběhlosti v matematice, dovedeme-li i z nejstručnějšího (ale správného) čtení správně si představiti nebo napsati slyšený výraz bez jakéhokoliv dalšího vysvětlování.

Plné čtení závorek, t. j. čtení první i druhé (uzavírací) závorky můžeme nahraditi čtverým způsobem.

První způsob. Výraz uzavřený do závorek čteme tak, jako kdyby nebyl v závorkách, a po přečtení výrazu dodáme „v závorce“, nebo méně často „v závorkách“. Čtení „v závorce“ není chybné, neboť v tomto případě můžeme považovati závorku za celek skládající se ze dvou částí, t. j. levé a pravé závorky. Ten[108]to způsob se hodí jen pro krátke výrazy, na př. pro dvojčleny nebo součiny jen několika málo čísel, a užívá se ho hlavně tehdy, jestliže se má výraz v závorkách uzavřený umocniti. Na př. (a+b)² čteme „á plus bé v závorce na druhou“, (3cx²y)³ čteme „tři cé iks na druhou ypsilon v závorce na třetí“, atp.

Druhý způsob. Je-li výraz uzavřený do závorek mnohočlen, ohlašujeme jej příslušným slovem, na př. dvojčlen, trojčlen atd. Slova mnohočlen nelze užíti, poněvadž ze slova má býti zřejmo, kolik členů mnohočlen má. Slovem dvojčlen (trojčlen atd.) upozorňujeme píšící osobu, aby napsala závorku, a zároveň jí předem udáváme počet členů, které budou mezi závorkami, takže po napsání posledního členu píšící osoba sama ihned výraz druhou závorkou uzavře. Způsob ten se hodí jen pro menší počet členů v mnohočlenu; při vyšším počtu členů by musil nejprve ten, kdo diktuje, zjistiti počet členů mnohočlenu, a osoba píšící by si musila pamatovati delší dobu, kolik členů má do závorek uzavříti. Příklady: 6x²—(3x+2)+5 čteme „šest iks na druhou minus dvojčlen — tři iks plus dvě — plus pět“; (4x³+2x2—10x—3) : (2x—3) můžeme čísti „čtyřčlen — čtyři iks na třetí plus dvě iks na druhou minus deset iks minus tři děleno dvojčlenem dvě iks minus tři“.

Třetí způsob. Je to výše (v 2. části) uvedené čtení „to celé“, které značí, že právě přečtený výraz je třeba celý uzavříti do závorek. Hodí se pro jakýkoliv výraz, je-li jasno, na co na vše se rčení „to celé“ vztahuje. Na př. (3cx²y)³ čteme „tři cé iks druhé ypsilon, to celé na třetí“.

Čtvrtý způsob. Je to způsob nejběžnější a záleží v tom, že při čtení děláme vhodné pomlčky, kratší nebo delší, jimiž rozdělujeme čtení na malé úseky, a při tom každý takový úsek čteme plynule. Každá pomlčka značí nějakou změnu v textu, nejčastěji ovšem závorku. Několik příkladů bylo uvedeno při dělení. Připojíme zde další příklady jiné. Mocninu (3cx²y)³ čteme „tři cé iks na druhou ypsilon — na třetí“. Kdybychom neudělali při čtení pomlčku, značilo by čtení výraz 3cx²y³. Součin [(x—y)²+ +3(x+2y)] (2x—5) čteme „iks minus ypsilon — na druhou — plus třikrát — iks plus dvě ypsilon — krát dvě iks minus pět“. Čtení „iks minus ypsilon na druhou plus třikrát iks plus dvě ypsilon krát dvě iks minus pět“ (vesměs bez pomlček) by značilo výraz x—y²+3(x+2y) (2x—5). Je vidět, že lze tohoto způsobu užíti téměř všude, a že pro vycvičený sluch nečiní porozumění takového čtení potíží. Ve zvláště složitých případech spojujeme tento způsob s přesným a úplným čtením některého znaku.

[109]Pomlčky vynecháváme, jestliže čteme nějakou poučku (větu nebo vzorec), při níž předpokládáme, že je poslouchající osobě známa. Rovněž vyslovujeme-li takovou poučku zpaměti. Na př. (a+b)² = a²+2ab+b² čteme (nebo vyslovíme) rychle a plynule „á plus bé na druhou rovná se á na druhou plus dvě á bé plus bé na druhou“.

Na konec uvedu čtení několika znaků z geometrie. Znak rovnoběžnosti jsou dvě svislé čárky, stejně dlouhé a stojící těsně u sebe (||). Jimi se označuje, že nějaký geometrický útvar je rovnoběžný s jiným útvarem. Čte se je rovnoběžný (-á, -é) nebo též rovnoběžno (s čím). Na př. m||n (m a n značí přímky) čteme „přímka em je rovnoběžná s přímkou en“, nebo stručně „em rovnoběžné (-o) s en“; také lze čísti „přímky em a en jsou spolu rovnoběžné“.

Znak kolmosti je obrácené velké písmeno T, t. j. vodorovná čárka a na ní čárka svislá (_┴). Čte se je kolmý (-á, -é, -o) nebo stojí kolmo (k čemu nebo na co). Na př. a _┴ b čteme „přímka á je kolmá k přímce bé“ nebo krátce „á kolmo k bé“. Podobně jako o rovnoběžnosti lze též říci „přímky á a bé stojí na sobě kolmo“ (nebo „jsou k sobě kolmé“). Čtení se ovšem nemění, i když jde o útvary nestejného druhu (na př. o přímku a rovinu).

Znak podobnosti (~) se čte je podobný (-á, -é, -o) nebo méně často podobá se (čemu). Na př. ∆ ABC ~ ∆ A'B'C' čteme „trojúhelník á bé cé je podobný (podobá se) trojúhelníku á s čarou, bé s čarou, cé s čarou“.

Znak shodnosti () se čte je shodný (-á, -é, -o), shoduje se (s čím).

Znak totožnosti (≡) se čte je totožný (-á, -é, -o), nebo i bez slova je. Na př. a ≡ m čteme „přímka á je totožná s přímkou em“ nebo stručně „á totožno s em“. Znaku totožnosti se užívá také k označení nějakého útvaru se zřetelem na jeho určující prvky. Na př. ρ ≡ (A, B, C) čteme „rovina ró je určena (dána) body á, bé, cé“; nebo σ ≡ (A, m) čteme „rovina sigma je určena bodem á a přímkou em“, atd. V obou smyslech užíváme znaku totožnosti též v aritmetice, algebře i v analyse. Na př. klademe jej mezi dva různé symboly, vyjadřující však stejný pojem. Nebo jej dáváme mezi symbol a nějakou funkci, abychom při odkazu na tuto funkci ji nemusili opisovati, nýbrž jen uvésti onen symbol.

Znak pro úhel (t. j. 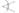) se dává před písmeno vyjadřující obecně úhel jen tehdy, jestliže by bez tohoto znaku mohlo dojíti k omylu. Čte se prostě úhel, na př. 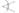γ „úhel gama“. Někdy se [110]úhel značí / a dává se nad písmeno značící úhel. Pravý úhel se označuje kromě čísla 90° buď jako R nebo ^π/₂ a čte se rozličně. Na př. α+β = R (nebo ^π/₂) můžeme čísti „alfa plus beta rovná se pravému úhlu“, nebo „…devadesáti stupňům“, nebo krátce „rovná se er (pí půl)“. Podobně čteme úhel přímý (180, 2R, π) a úhel plný (360°, 4R, 2π). Ostatní úhly vyjadřujeme nejčastěji ve stupních (°), minutách (') a vteřinách ("). Na př. úhel 39°17'28" čteme „třicet devět stupňů, sedmnáct minut, dvacet osm vteřin (sekund)“.

Úsečka se někdy značí vodorovnou přímkou nad písmeny udávajícími oba koncové body úsečky. Na př. 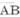 čteme „úsečka á bé“. Podobně se značí oblouk mezi dvěma body, na př.  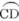a čte se „oblouk cé dé“.

Je ještě hodně znaků, jejichž čtení nebylo zde uvedeno, ale tyto znaky nejsou již tak běžné v obecném životě, takže by nemělo velkého užitku zmiňovati se o tom v Naší řeči. Bylo by však dobře, kdyby se tomuto námětu věnovala dostatečná pozornost, zejména na školách, aby řeč v matematice byla nejen stručná a jasná po stránce čistě matematické, ale aby byla také, pokud je to jen možno, i jazykově správná.

Naše řeč, ročník 22 (1938), číslo 4, s. 101-110

Předchozí Josef Beneš: Předložka na při jménech osad

Následující Miloslav Wajs: Čestné názvy středních škol